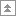Методика корреляционного анализа

2) Ранговый метод

· составить два ряда из парных сопоставляемых признаков, обозначив первый и второй ряд соответственно х и у. При этом представить первый ряд признака в убывающем или возрастающем порядке, а числовые значения второго ряда расположить напротив тех значений первого ряда, которым они соответствуют

· величину признака в каждом из сравниваемых рядов заменить порядковым номером (рангом). Рангами, или номерами, обозначают места показателей (значения) первого и второго рядов. При этом числовым значениям второго признака ранги должны присваиваться в том же порядке, какой был принят при раздаче их величинам первого признака. При одинаковых величинах признака в ряду ранги следует определять как среднее число из суммы порядковых номеров этих величин

· определить разность рангов между х и у (d): d = х - у

· возвести полученную разность рангов в квадрат ()

· получить сумму квадратов разности () и подставить полученные значения в формулу:

(

Схема оценки корреляционной связи по коэффициенту корреляции

Вычисление ошибки коэффициента корреляции

· ошибка коэффициента корреляции, вычисленного методом квадратов (Пирсона):

(10)

· ошибка коэффициента корреляции, вычисленного ранговым методом (Спирмена):

(11)

Оценка достоверности коэффициента корреляции, полученного методом ранговой корреляции и методом квадратов

Способ 1.

Достоверность определяется по формуле:

или (12)

Критерий t оценивается по таблице значений t с учетом числа степеней свободы (n - 2), где n - число парных вариант. Критерий t должен быть равен или больше табличного, соответствующего вероятности р ≥99%.

Способ 2.

Достоверность оценивается по специальной таблице стандартных коэффициентов корреляции. При этом достоверным считается такой коэффициент корреляции, когда при определенном числе степеней свободы (n - 2), он равен или более табличного, соответствующего степени безошибочного прогноза р ≥95%.

Другие материалы

Анализ оборотных средств ООО ВОСТОК-СЕРВИС
Оборотный капитал являются одной из составных частей имущества предприятия. Состояние и эффективность их использования - одно из главных условий успешной его деятельности. Развитие рыночных отношений определяет новые условия ...

Анализ и экономическая оценка эффективности использования основных фондов предприятия ООО Гостиный двор-2001
Основные фонды представляют собой объекты имущества организации, используемые в качестве средств труда при производстве продукции, выполнении работ и оказании услуг, либо для управления организацией в течение периода, превышающего 12 месяце ...