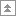Корреляционно-регрессионный анализ показателей социального развития республики Бурятия
Для определения параметров уравнения регрессии построим расчетную таблицу:
Таблица 5 - Расчет параметров регрессии уравнения прямой линии
|
дата |
y, Численность населения - всего, тыс. человек, в том числе: |
x , Число больничных учреждений |
x^2 |
xy |
|
2000 |
1004,80 |
115 |
13225 |
115552 |
|
2001 |
996,90 |
117 |
13689 |
116637,3 |
|
2002 |
981,23 |
122 |
14884 |
119710,06 |
|
2003 |
979,60 |
122 |
14884 |
119511,2 |
|
2004 |
974,30 |
121 |
14641 |
117890,3 |
|
2005 |
969, 20 |
111 |
12321 |
107581,2 |
|
2006 |
963,30 |
54 |
2916 |
52018,2 |
|
2007 |
960,00 |
53 |
2809 |
50880 |
|
2008 |
959,90 |
51 |
2601 |
48954,9 |
|
2009 |
960,70 |
44 |
1936 |
42270,8 |
|
2010 |
971,30 |
46 |
2116 |
44679,8 |
|
2011 |
971, 20 |
47 |
2209 |
45646,4 |
|
2012 |
971,30 |
47 |
2209 |
45651,1 |
|
сумма |
12663,73 |
1050,00 |
100440,00 |
1026983,26 |
Для определения параметров уравнения регрессии подставим в систему нормальных уравнений фактические данные из таблицы:
Далее решаем систему нормальных уравнений и получаем следующие коэффициенты уравнения регрессии:
= 952,7242 и 
= 0,2651
Таким образом, уравнение регрессии примет следующий вид:
= 0,27х+952,72
Параметр
показывает усредненное влияние на результативный признак неучтенных, т.е. не выделенных для исследования факторных признаков. Экономического смысла не имеет, т.к. неизвестно, сколько факторов и как каждый из них влияет на изменения результативного признака.
Другие материалы
Неоклассическая версия теории предельной полезности
В последней трети 19в. В Австрии, США, Англии произошел подлинный
переворот в экономической теории: возникло НЕОКЛАССИЧЕСКОЕ (по греч. неос -
новый). Основу неоклассической теории составили разработки 3-х научных школ:
австри ...
Организация финансово-экономической деятельности ООО Лениногорское управление тампонажных работ
ОБЩЕЕ ОЗНАКОМЛЕНИЕ С ПРЕДПРИЯТИЕМ
...
Главное меню
